To run a TRUST simulation, all you have to do is write a correctly formatted data file. This is one of the advantages offered by the platform, allowing the user to change, modify, and test calculations without needing to write C++ code or recompile/link with the TRUST library. However, there is a specific syntax that must be respected to ensure that the TRUST interpreter can read the data file correctly and perform the necessary calculations.
Attention: TRUST is sensitive to empty spaces. To avoid issues, use an empty space before and after each keyword. For example, Read_MED{domain dom file Mesh.med} won’t work! You should write Read_MED { domain dom file Mesh.med } (note the spaces before and after the braces { ... }).
Attention: It is possible to write comments in you data file. This can be done by the # character; # at the begining and at the end of the commented line/paragraph. It is also possible to put your comments between /* and */, as the bloc comments in C++. Again, attention to the empty spaces. See these examples:
# THIS IS A COMMENT #
/* THIS ALSO */
/* THESE
ARE
ALSO
COMMENTS */
# THESE
TOO
...
YES ! #
#THIS IS NOT GOOD! NEED SPACES#
/*THIS IS BAD TOO*/
// THIS IS NOT POSSIBLE NOOO
# THIS IS NOT POSSIBLE BECAUSE IT IS NOT CLOSED
/* NEITHER IS THIS
In this section, we will consider an example of a test case where all the steps required to write the corresponding data file will be detailed. The selected example is a 2D flow around a square obstacle in an open domain (Von Karman vortex street). We recommend to use the SI units for all quantities (velocity, viscosity, etc.).
Step 1: Create an empty data file
Create an empty data file named Obstacle.data in an empty Obstacle repository.
Step 2: Create your mesh
Prepare a meshed domain that will be used in the simulation. In this example, a mesh named Mesh defined on a domain named dom and written in a MED file named Mesh.med is used. The MED file includes five boundaries:
- Square: representing the obstacle
- Upper: representing the upper-top boundary
- Lower: representing the lower-bottom boundary
- Inlet: representing the inlet-left boundary
- Outlet: representing the outlet-right boundary
It is important to note the names of all the boundaries because they will need to be specified when imposing boundary conditions. Here is a visualization of the mesh used in the simulation.
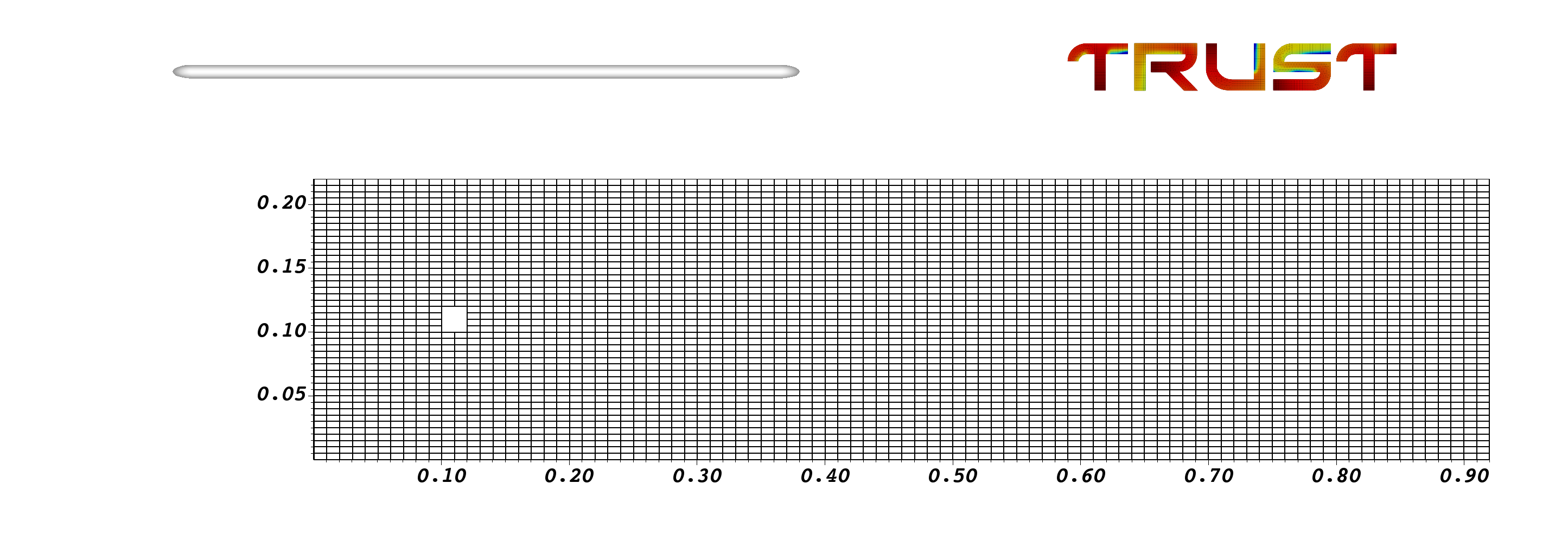
Now, you can start constructing your data file.
Note: You can get the Mesh.med file used in this section by doing
wget https://github.com/cea-trust-platform/cea-trust-platform.github.io/blob/master/images/simulation/Mesh.med
Step 3: Define the domain and read the mesh
You should start by defining the dimension of the domain. In this case it is 2D.
You should then create an instance of the Domaine class, named dom as that you used in the MED file.
Read the MED file and the mesh using the class Read_MED. Since the generated mesh was a bit coarse, TRUST allows you to refine the mesh if you like to. This can be done via the class Raffiner_isotrope applied to your domain dom.
Start by inserting this in Obstacle.data
# Dimension can be 2D or 3D #
dimension 2
# Domain definition #
Domaine dom
# Read the mesh from MED file #
Read_MED { domain dom file Mesh.med }
# Refine the mesh to have better results (optional) #
Raffiner_isotrope dom
Step 4: Define the discretization and the problem
The mesh used here allow us to use the VDF discretization. So use the class VDF to create an instance with the variable my_discretisation.
We will solve just the Navier-Stokes (NS) equations, so it is a hydraulic problem. Create an instance of Pb_hydraulique and name it pb.
Insert this in Obstacle.data
# Discretization on rectangles (hexa), so use VDF #
VDF my_discretisation
# Problem definition #
Pb_hydraulique pb
Step 5: Define the time integration scheme
Its for you to define what time scheme to use. Here, we will use the Euler explicit scheme. For that, we create an instance of Scheme_euler_explicit, I called it my_scheme, and we read its parameters.
This bloc contains a lot of parameters, try to read the comments and insert the bloc in Obstacle.data.
# Define your time scheme; here use explicit #
Scheme_euler_explicit my_scheme
Read my_scheme
{
# Initial time [s] #
tinit 0
# Min time step #
dt_min 5.e-6
# Max time step #
dt_max 5.e-3
# facsec such as dt = facsec * min(dt(CFL),dt_max) ; for explicit scheme facsec <= 1. By default facsec equals to 1 #
facsec 0.5
# Output criteria #
# .out files printing period #
dt_impr 5.e-3 # Note: small value to print at each time step #
# End time [s] of the simulation #
tmax 10.0
}
Step 6: Assosciate the instantiated objects
Now, you need to link the domaine, the discretization and the time scheme to the problem. This is done by the C++ class Associate and Discretize.
Insert this in Obstacle.data
# Association between the different objects #
Associate pb dom /* Assosciate domaine */
Associate pb my_scheme /* Assosciate time scheme */
Discretize pb my_discretisation /* Discretize the domain */
Step 7: Read the problem (medium, equation, BC’s, post-processings)
That’s the main point now: define the problem!
Start by defining the incompressible medium Fluide_incompressible.
Once done, read the Navier-Stokes equation Navier_Stokes_standard. Provide the pressure solver Solveur_pression and the spatial scheme to be used for the convection operator (here we use the third order Quick scheme).
Precise the initial and boundary conditions. This is done by the Initial_conditions and Boundary_conditions keywords. Here, we consider that the fluid is at rest at the initial state; so the velocity field is null. At the boundaries, we consider a no-slip BC at the obstacle borders and symmetry at the top/bottom walls. At the inlet, we fix the horizontal velocity to 1 m/s, while the pressure is fixed at the outlet (open boundary).
Finally, ask TRUST to write you the velocity and vorticity fields to visualize them after! Thus, create and read a Post_processing object.
Try to read carefully the syntax/comments and insert the bloc in Obstacle.data.
# Problem description #
Read pb
{
# Physical characteristcs of medium #
Fluide_incompressible
{
# Dynamic viscosity [kg/m/s] #
mu Champ_Uniforme 1 3.7e-05
# Volumic mass [kg/m3] #
rho Champ_Uniforme 1 2
}
# NS equation #
Navier_Stokes_standard
{
# Pressure matrix solved with #
Solveur_pression PETSc Cholesky { }
# Solve the convection operator with a 3rd order QUICK scheme #
Convection { quick }
# Solve the diffusion too; remember diffusion always 2nd order centered #
Diffusion { }
# Uniform initial condition for velocity #
Initial_conditions { vitesse Champ_Uniforme 2 0. 0. }
# Boundary conditions #
Boundary_conditions
{
Square paroi_fixe
Upper symetrie
Lower symetrie
Outlet frontiere_ouverte_pression_imposee Champ_front_Uniforme 1 0.
Inlet frontiere_ouverte_vitesse_imposee Champ_front_Uniforme 2 1. 0.
}
}
# Post_processing description #
Post_processing
{
# Fields #
format lata
fields dt_post 1.e-2
{
vitesse som
vorticite som
}
}
}
Step 8: Solve the problem!
Now, end your data file by inserting this bloc. This will tell TRUST to run and solve the problem.
# The problem is solved with #
Solve pb
Save your Obstacle.data file and run the simulation by doing:
trust Obstacle.data
Results! It’s cool 🍻🤗🍻
Now, you can visualize your results! You should see an animation similar to the one shown below! It is the well known Von Karman vortex street!

Also, check out our YouTube channel. Don’t forget to like the page! 😜
The complete data file
# Dimension can be 2D or 3D #
dimension 2
# Domain definition #
Domaine dom
# BEGIN MESH #
Read_MED { domain dom file Mesh.med }
raffiner_isotrope dom
# END MESH #
# BEGIN PARTITION
Partition dom
{
/* Choose Nb_parts so to have ~ 25000 cells per processor */
Partition_tool metis { nb_parts 2 }
Larg_joint 2
zones_name DOM
}
End
END PARTITION #
# BEGIN SCATTER
Scatter DOM.Zones dom
END SCATTER #
# Discretization on hexa or tetra mesh #
VDF my_discretisation
# Problem definition #
Pb_hydraulique pb
# Time scheme explicit or implicit #
Scheme_euler_explicit my_scheme
Read my_scheme
{
# Initial time [s] #
tinit 0
# Min time step #
dt_min 5.e-6
# Max time step #
dt_max 5.e-3 # dt_min = dt_max so dt imposed #
# facsec such as dt = facsec * min(dt(CFL),dt_max) ; for explicit scheme facsec <= 1. By default facsec equals to 1 #
facsec 0.5
# make the diffusion term in NS equation implicit : disable(0) or enable(1) #
diffusion_implicite 0
# Output criteria #
# .out files printing period #
dt_impr 5.e-3 # Note: small value to print at each time step #
# .sauv files printing period #
dt_sauv 100
periode_sauvegarde_securite_en_heures 23
# Stop if one of the following criteria is checked: #
# End time [s] #
tmax 10.0
# Max number of time steps #
# nb_pas_dt_max 3 #
# Convergence threshold (see .dt_ev file) #
seuil_statio 1.e-8
}
# Association between the different objects #
Associate pb dom
Associate pb my_scheme
Discretize pb my_discretisation
# Problem description #
Read pb
{
# Physical characteristcs of medium #
fluide_incompressible
{
# Dynamic viscosity [kg/m/s] #
mu Champ_Uniforme 1 3.7e-05
# Volumic mass [kg/m3] #
rho Champ_Uniforme 1 2
}
# NS equation #
Navier_Stokes_standard
{
# Pressure matrix solved with #
/* solveur_pression GCP
{
precond ssor { omega 1.500000 }
seuil 1.000000e-06
impr
} */
solveur_pression Cholesky { }
# Two operators are defined #
convection { quick }
diffusion { }
# Uniform initial condition for velocity #
initial_conditions { vitesse Champ_Uniforme 2 0. 0. }
# Boundary conditions #
boundary_conditions
{
Square paroi_fixe
Upper symetrie
Lower symetrie
Outlet frontiere_ouverte_pression_imposee Champ_front_Uniforme 1 0.
Inlet frontiere_ouverte_vitesse_imposee Champ_front_Uniforme 2 1. 0.
}
}
# Post_processing description #
Post_processing
{
# Probes #
Probes
{
# Note: periode with small value to print at each time step (necessary for spectral analysis) #
sonde_pression pression periode 0.005 points 2 0.13 0.105 0.13 0.115
sonde_vitesse vitesse periode 0.005 points 2 0.14 0.105 0.14 0.115
sonde_vit vitesse periode 0.005 segment 22 0.14 0.0 0.14 0.22
sonde_P pression periode 0.01 plan 23 11 0.01 0.005 0.91 0.005 0.01 0.21
/* sonde_Pmoy Moyenne_pression periode 0.005 points 2 0.13 0.105 0.13 0.115
sonde_Pect Ecart_type_pression periode 0.005 points 2 0.13 0.105 0.13 0.115 */
}
# Fields #
format lata
fields dt_post 1.e-2 # Note: Warning to memory space if dt_post too small #
{
/* pression elem
pression som
vitesse elem
vitesse som */
vorticite som
}
# Statistical fields #
/* Statistiques dt_post 1.
{
t_deb 1. t_fin 5.
moyenne vitesse
ecart_type vitesse
moyenne pression
ecart_type pression
} */
}
# Saving and restarting process #
/* resume_last_time binaire datafile.sauv */
}
# The problem is solved with #
Solve pb
# Not necessary keyword to finish #
End



