HOW TO DEFINE A STATIONNARY TEST-CASE ?

L’objectif ici est de mettre en place un cas-test stationnaire. Par stationnaire, on entend que seul le resultat stabilise (donc en fin de transitoire) est digne d’interet et d’analyse. Dans ce type de cas tests, seuls les resultats stationnaires finaux sont justes. Les resultats obtenus pendant la periode transitoire permettant d’obtenir l’etat stationnaire final ne sont, quant a eux, pas forcement justes et ne doivent pas etre analyses.

Prenons l’exemple de la modelisation d’une cavite carree avec une paroi superieure defilante (vitesse imposee sur la paroi superieure en monophasique. La mise en mouvement de la paroi superieure va creer un tourbillon principal au centre de la cavite avec des recirculations au niveau des 2 angles inferieurs.

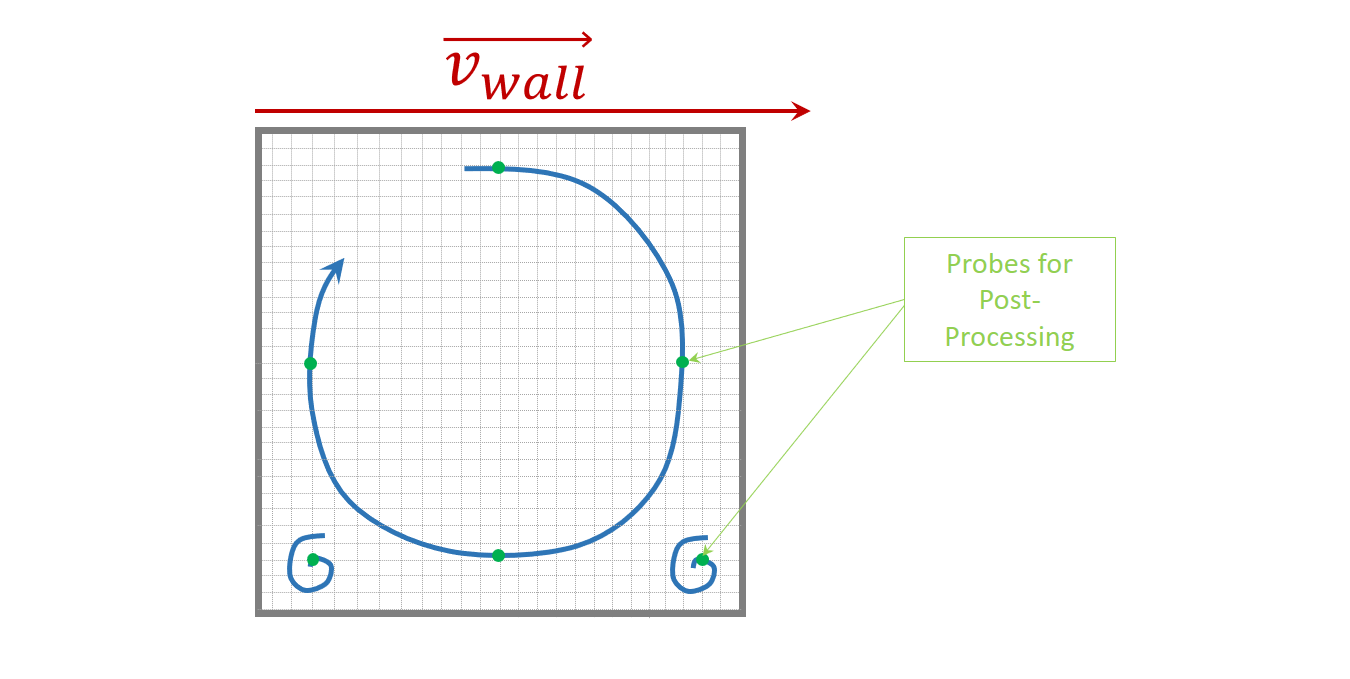
Figure 1 Etat stationnaire attendu pour un ecoulement dans une cavite carree a laquelle une vitesse est imposee sur la paroi superieure

Les etapes pour definir ce type de calcul sont les suivantes :

• Le maillage : pour bien prendre en compte la vitesse imposee de la paroi superieure, il est necessaire de definir un maillage suffisamment fin a ce niveau. Il est egalement necessaire de raffiner le maillage sur les autres bords du domaine afin que les forces de frottement soient bien calculees. On definira donc une maillage raffine sur les bords du domaine et un maillage plus grossier en son centre.

• La physique resolue : le probleme resolu ici est un probleme laminaire qui sera definit avec le mot cle Pb_thermohydraulique.

• Les proprietes des fluides : dans le cas d’un probleme isoterme, les proprietes des fluides doivent etre definis a la temperature et a la pression du probleme considere (ces valeurs sont a rechercher dans les tableaux d’Etat).

• Le schema de convection : dans ce cas de figure, le choix du schema est important. Il s’agit de trouver un compromis entre un schema trop grossier et un schema trop fin. Si on utilise un schema grossier du er ordre, les petits tourbillons atendus dans les angles inferieurs de la cavite seront ecrases par la viscosite numerique. En revanche, si le schema est trop precis (comme un schema de type centre), des oscillations parasites risquent d’apparaitre. Dans le cas d’une discretisation VDF, on priviligera un schema de type quick et en VEF un schema muscl.

• Le schema de diffusion : dans un cas stationnaire laminaire, il n’est pas necessaire de definir un schema de diffusion.

• Le schema en temps : pour obtenir les resultats d’un cas stationnaire, le solveur a utiliser sera un solveur implicite. L’objectif de ce type de calcul est d’obtenir un resultat juste une fois le transitoire stabilise et non pas de comprendre et d’etudier la phenomenologie du transitoire. Durant la periode transitoire, les resultats obtenus ne seront pas forcement “justes” et ne doivent pas etre interpretes et analyses. Seuls les resultats finaux sont garantis et dignes d’interet. Nous recommandons d’utiliser un schema Euler implicite avec un schema GMRES pour la vitesse et un schema GCP (gradients conjugues PETSC) pour la pression. Dans la definition du schema en temps, il est recommande de commencer avec dt_min 1e-5. Le dt_min n’a aucun rapport avec la physique consideree, il permet juste d’imposer un pas de temps minimum au solveur afin d’eviter les chutes de pas de temps. Il est egalement recommande de definir un pas de temps pour l’impression des resultats dt_impr = dt_min afin d’avoir en permanence un suivi du calcul. Les impressions obtenues seront visible dans les fichiers de sortie .out et .err. Il est egalement recommande de commence le calcul avec un premier pas de temps qui ne bouge pas afin d’avoir une meilleure initialisation dt_start dt_fixe 1e-3 et de definir un facteur de XXXX de 10 fac_sec 10. qui multiplie par 10 les pas de temps de la convection et de la diffusion.

• Le post-traitement : pour analyser les resultats obtenus, il est necessaire de passer par un bloc de post-traitement dans lequel nous definirons des sondes avec un format de sortie en lata. Ces sondes devront etre definies sur des grandeurs pertinentes pour le calcul considere (ici les sondes porteront sur la vitesse et la pression) mais egalement en des endroits pertinents pour la geometrie consideree. Ici les zones d’interet se situent pres des parois mais egalement dans les coins inferieurs ou des zones de recirculation vont vraissemblablement apparaitre. Dans cette phase de construction du jeu de donnees, il est recommande de definir la frequence choisie pour les resultats de sortie toutes les secondes.

Une premiere version du jeu de donnees est alors constituee et le calcul peut etre lance sur 3 secondes, permettant ainsi d’avoir 3 sorties lata pour les differents champs definis. Il est important de s’assurer que tout fonctionne correctement en verifiant, tout d’abord que ce calcul preliminaire se termine bien.

Si le calcul preliminaire ne tourne pas, le premier reflexe est de regarder le message d’erreur dans le .err. Si, a ce stade, le calcul n’a pas abouti, il est fort probable qu’il y ait un probleme de convergence. On regarde alors les valeurs des pas de temps de stabilite, a la fois pour la convection et la diffusion, dans le fichier de sortie .out. Si les valeurs des pas de temps de stabilite sont tres petites (< dt_min), il est alors necessaire de diminuer la valeur du dt_min jusqu’a ce que le calcul tourne.

Si le calcul preliminaire se termine avec succes, on regarde alors les pas de temps de stabilite pour la convection et la diffusion dans le fichier de sortie .out afin d’adpater en consequence le dt des fichiers de post-traitement (lata). On relancera le calcul sur 1000 pas de temps e, ayant veille a augmenter la frequence de sauvegarde des sondes a 100 pas de temps (contre toutes les secondes lors du calcul preliminaire). Avec cette nouvelle definition des PdT, nous obtiendrons 10 resultats des sondes (lata) donnant, d’ores et deja, une bonne impression de l’avancee du calcul.

Si les phenomenes physiques sont en plein developpement, c’est-a-dire que la vitesse de chaque sonde n’a pas atteint la stabilite, on augmente alors le temps du calcul (tmax) en veillant bien a adapter la frequence des lata en consequence et on relance alors le calcul. On reitere cette etape en surveillant le developpement de l’ecoulement a travers les sondes et les lata. On reiterera cette etape autant de fois que necessaire jusqu’a l’obtention de l’etat stationnaire du probleme. Cet etat stationnaire est atteint lorsque l’evolution de la vitesse sur toutes les sondes doit etre constante. En observant les pas de temps dans le fichier de sortie .out, on constate que TrioCFD va augmenter progressivement les pas de temps car il sait que la solution recherchee est une solution stationnaire, de par le schema en tempds defini et va donc de plus en plus vite pour atteindre cet etat.

Afin de s’assurer de l’obtention de cet etat stationnaire, il est recommande de s’interesser aux residus. Ceux-ci (accessibles dans le fichier de sortie .out) doivent decroitre sur la pression et la vitesse.

Warning

Parfois, cette decroissance n’a pas lieu et peut venir soit de la presence de petits tourbillons qui se sont developpes dans l’ecoulement soit d’une mauvaise resolution d’une ou de plusieurs mailles du domaine.

Typiquement, dans le cas de figure considere ici, il convient de porter une attention toute particuliere a la maille dans l’angle superieur droit du domaine car il s’agit du point de rencontre entre une paroi fixe et la paroi superieure mobile. Il convient alors de determiner d’ou ces residus proviennent et comment ils se stabilisent. Dans cet exemple-ci, ils seront donc purement numeriques et ne signifieront pas forcement qu’il y a un probleme physique.