Thermal modeling

Thermal modeling#

There are 3 types of thermal fluxes available in TrioCFD multiphase:

  • The interfacial heat flux \(h_k(\alpha,T,P)\)

  • The wall heat flux \(q_{pk}(\alpha,T,P)\)

  • The phase change flux \(G(\alpha,T,P)\)

The computation of condensation and evaporation is done in Source_Flux_interfacial_base:

void Source_Flux_interfacial_base::set_param(Param& param)
{
  const Pb_Multiphase& pbm = ref_cast(Pb_Multiphase, equation().probleme());
  if (!pbm.has_correlation("flux_interfacial"))
    Process::exit(que_suis_je() + ": a flux_interfacial correlation must be defined in the global correlations { } block!");

  correlation_ = pbm.get_correlation("flux_interfacial");

  dv_min = ref_cast(Flux_interfacial_base, correlation_->valeur()).dv_min();

  return is;
}

with \(\texttt{n_lim}=\begin{cases} -1,\ \text{if G won't make the phase evanescent}\\ \text{number of the evanescent phase, otherwise.} \end{cases}\)

If saturation activated then:

(181)#\[\begin{equation} \newcommand {\parent} [1] {\left( #1 \right)} \newcommand{\pluseq}{\mathrel{+}=} \newcommand{\minuseq}{\mathrel{-}=} \newcommand{\timeseq}{\mathrel{*}=} \Phi=h_g(T_g-T_{sat})+h_l(T_l-T_{\text{sat}})+q_p \end{equation}\]
(182)#\[\begin{equation} L=\begin{cases} h_l-H_{ls},\text{ if } \Phi<0\\ h_g-H_{gs},\text{ otherwise}. \end{cases} \end{equation}\]

If no correlation for G or if \(|\frac{\Phi}{L}|<|G|\) (limitation by energy conservation) then:

(183)#\[\begin{equation} G=\frac{\Phi}{L} \end{equation}\]

The phase change G is limited by evanescence at \(G_{\text{lim}}\) (see evanescence part).

(184)#\[\begin{equation} h_g=\begin{cases} h_g,\text{ if }0<G, \\ H_{ls},\ \text{otherwise}. \end{cases} \end{equation}\]
(185)#\[\begin{equation} h_l=\begin{cases} h_l,\text{ if }G<0, \\ H_{vs},\ \text{otherwise}. \end{cases} \end{equation}\]
(186)#\[\begin{equation} \frac{dh_g}{dT_g}=\begin{cases}\frac{dh_g}{dT_g},\text{ if }0<G, \\ 0,\ \text{otherwise}. \end{cases} \end{equation}\]
(187)#\[\begin{equation} \frac{dh_l}{dT_l}=\begin{cases}\frac{dh_l}{dT_l},\text{ if } G<0, \\ 0,\ \text{otherwise}. \end{cases} \end{equation}\]
(188)#\[\begin{equation} \frac{dh_g}{dP}=\begin{cases}\frac{dh_g}{dP},\text{ if }0<G, \\ \frac{dh_{ls}}{dP},\ \text{otherwise}. \end{cases} \end{equation}\]
(189)#\[\begin{equation} \frac{dh_l}{dP}=\begin{cases}\frac{dh_l}{dP},\text{ if }G<0, \\ \frac{dh_{vs}}{dP},\ \text{otherwise}. \end{cases} \end{equation}\]

If there is no evanescence and no phase change model then:

(190)#\[\begin{equation} \frac{d\Phi}{dP}=\frac{dh_g}{dP}\parent{T_g-T_{sat}} + \frac{dh_l}{dP}\parent{T_l-T_{sat}} - \frac{dT_sat}{dP}(h_g-h_{l})+\frac{dq_p}{dP}\frac{1}{vol} \end{equation}\]
(191)#\[\begin{equation} \frac{dG}{dP}=\frac{\frac{d\Phi}{dP}-G\frac{dL}{dP}}{L} \end{equation}\]
(192)#\[\begin{equation} \frac{dG}{dT}=\frac{1}{L}\parent{\frac{dh_g}{dT}(T_g-T_{sat})+\frac{dh_l}{dT}(T_l-T_{sat})+\frac{dq_p}{dT}+\begin{cases}h_g-G\frac{dL}{dT_g},\text{ if in gas phase} \\ h_l-G\frac{dL}{dT_l},\ \text{otherwise} \end{cases}} \end{equation}\]
(193)#\[\begin{equation} \frac{dG}{d\alpha}=\frac{1}{L}\Bigg(\frac{dh_g}{d\alpha}(T_g-T_{sat}+\frac{dh_l}{d\alpha}(T_l-T_{sat})+\frac{dq_p}{d\alpha}) \Bigg) \end{equation}\]

These fluxes are then distributed to the following equations:

  • Mass equation as source/sink

  • Energy equation as heat transfer

  • Interfacial area concentration as condensation/nucleation (cf equivalent diameter section)

The model is implemented as follows:

  • In the energy equation:

(194)#\[\begin{align} &h_m=\frac{1}{\frac{1}{h_g} + \frac{1}{h_l}} \\ &\text{secmem} \minuseq h_m(T_g-T_l)\times \begin{cases} -1,\text{ for the liquid,} \\ 1,\ \text{otherwise}. \end{cases}.\\ &M_T \minuseq h_m\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}\times \begin{cases} 1,\text{ regarding the same phase}, \\ -1,\text{ otherwise}. \end{cases}. \end{align}\]

If saturation is activated, then in the mass equation we get:

(195)#\[\begin{equation} \texttt{secmem} \minuseq G\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}. \end{equation}\]

if there is no evanescence then:

(196)#\[\begin{equation} M_\alpha \pluseq \frac{dG}{d\alpha}\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}. \end{equation}\]
(197)#\[\begin{equation} M_T \pluseq \frac{dG}{dT}\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}. \end{equation}\]
(198)#\[\begin{equation} M_P \pluseq \frac{dG}{dP}\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}. \end{equation}\]

If saturation is activated, then in the energy equation we get:

(199)#\[\begin{equation} \texttt{secmem} \minuseq \parent{\texttt{signflux}\times h_c(T_c-T_{sat}) + Gh_c}\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases} + \begin{cases} q_p,\text{ if not c}, \\ 0,\text{ otherwise}. \end{cases}. \end{equation}\]
(200)#\[\begin{equation} \begin{aligned} M_\alpha \pluseq \parent{\texttt{signflux}\times \frac{dh_c}{d\alpha}(T_c-T_{sat})+h_c\frac{dG}{d\alpha}\begin{cases} 0,\text{ if evanescent},\\ 1,\text{ otherwise}. \end{cases}}\times & \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases} & \\- \begin{cases} \frac{dq_p}{d\alpha},\text{ if not c}, \\ 0,\text{ otherwise}. \end{cases}. \end{aligned} \end{equation}\]
(201)#\[\begin{equation} \begin{aligned} M_T \pluseq \parent{\texttt{signflux}\times \parent{\frac{dh_c}{dT}(T_c-T_{sat})+h_c\begin{cases} 1, if\ n_c,\\ 0,\text{ otherwise}. \end{cases}}& + & \\h_c\frac{dG}{dT}\begin{cases} 0, if\ evanescent,\\ 1,\text{ otherwise}. \end{cases} + G\frac{dh_c}{dT}\begin{cases} \frac{dq_p}{d\alpha},\ if\ n_c, \\ 0,\text{ otherwise}. \end{cases}}\times &\begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}& \\ - \begin{cases} \frac{dq_p}{dT},\text{ if not c}, \\ 0,\text{ otherwise}. \end{cases}. \end{aligned} \end{equation}\]
(202)#\[\begin{equation} \begin{aligned} M_P \pluseq \parent{\texttt{signflux}\times \Big(\frac{dh_c}{dP}(T_c-T_{sat})+h_c\frac{dT_{sat}}{dP}\Big)+h_c\frac{dG}{dP}\begin{cases} 0,\text{ if evanescent},\\ 1,\text{ otherwise}. \end{cases}& +& \\G\frac{dh_c}{dP}}\times \begin{cases} -1,\text{ for the liquid}, \\ 1,\text{ otherwise}. \end{cases}-\begin{cases} \frac{dq_p}{d\alpha},\text{ if not c}, \\ 0,\text{ otherwise}. \end{cases}. \end{aligned} \end{equation}\]

with \(c\) the minority phase side to respect the energy conservation in case of evanescence.

Interfacial heat flux#

The general expression of the interfacial heat flux is:

(203)#\[\begin{equation} \phi_{kl}=h_{kl}(T_k - T_l) \end{equation}\]

The model is implemented in:

void Flux_interfacial_base::set_param(Param& param)

The available input parameters are:

    double dh;            // Hydraulic diameter
    const double *alpha;  // Void fraction
    const double *T;      // Temperature
    const double *T_passe;// Previous time temperature
    double p;             // Pressure
    const double *nv;     // Norme of relative velocity
    const double *lambda; // Thermal conductivity
    const double *mu;     // Viscosity
    const double *rho;    // Density
    const double *Cp;     // Calorific capacity
    const double *Lvap;   // Latent heat
    const double *dP_Lvap;// Phase change latent heat
    const double *h;      // Enthalpy
    const double *dP_h;   // Enthalpy derivative regarding pressure
    const double *dT_h;   // Enthalpy derivative regarding temperature
    const double *d_bulles;//Bubble diameter
    const double *k_turb; // Turbulent kinetic energy
    const double *nut;    // Turbulent viscosity
    const double *sigma;  // Superficial tension
    DoubleTab v;          // Velocity
    int e;                // Element index

The interfacial heat flux operator must fill hi tab so that:

  • \(\texttt{hi}({\color{myteal}k1}, {\color{mydarkorchid}k2})\) and \(\texttt{hi}({\color{mydarkorchid}k2},{\color{myteal}k1})\) exchange coefficients

  • \(\texttt{dT_hi}({\color{myteal}k1}, {\color{mydarkorchid}k2},n)\) and \(\texttt{dT_hi}({\color{mydarkorchid}k2},{\color{myteal}k1},n)\) Exchange coefficient derivative regarding the temperature

  • \(\texttt{da_hi}({\color{myteal}k1}, {\color{mydarkorchid}k2}, n)\) and \(\texttt{da_hi}({\color{mydarkorchid}k2}, {\color{myteal}k1}, n)\) Exchange coefficient derivative regarding void fraction of phase n

  • \(\texttt{dp_hi}({\color{myteal}k1}, {\color{mydarkorchid}k2})\) and \(\texttt{dp_hi}({\color{mydarkorchid}k2}, {\color{myteal}k1})\) Exchange coefficient derivative regarding pressure

Availability of drift models in TrioCFD/CMFD.

Model

Used

Validated

Test case

Constant

Yes

Yes

TrioCFD/CoolProp, TrioCFD/Gabillet, TrioCFD/Canal axi two-phase, Trust/Canal bouillant two-phase, Trust/Canal bouillant drift, Trust/Comparaison lois eau

Chen-Mayinger

Yes

No

Kim-Park

Yes

No

Ranz-Marshall

Yes

No

Wolfert

Yes

No

Wolfert compsant

Yes

No

Zeitoun

Yes

No

Constant#

The model is implemented in:

void Flux_interfacial_Coef_Constant::set_param(Param& param)
{
param.ajouter(pbm.nom_phase(n), &h_phase(n), Param::REQUIRED);
}

Default values: ?

The model implemented is:

(204)#\[\begin{equation} \texttt{hi}(k, l) = \texttt{h_phase}(k); \end{equation}\]

Chen and Mayinger#

The model is implemented in:

void Flux_interfacial_Chen_Mayinger::set_param(Param& param)

Default values: ?

The model implemented is:

(205)#\[\begin{equation} Nu=0.185Re_b^{0.7}Pr^{0.5}, \end{equation}\]
(206)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu\times\frac{\lambda_l}{d_b} \frac{6\times \max(\alpha_g, 1e-4)}{d_b}, \end{equation}\]
(207)#\[\begin{equation} \texttt{da_hi(n_l, k, k)}= \begin{cases} Nu \frac{6\lambda_l}{d_b^2},\text{ if }\alpha_g> 1e-4,\\ 0,\text{ otherwise} \end{cases} \end{equation}\]
(208)#\[\begin{equation} \texttt{hi(k, n_l)} = 1e8, \end{equation}\]

with

  • \(Re_b=\frac{\rho_l d_b (u_g-u_l)}{\mu_l}\)

  • \(Pr\frac{\mu_l Cp_l}{\lambda_l}\)

Kim and park#

The model is also described in REFNEC and is implemented in:

void Flux_interfacial_Kim_Park::set_param(Param& param)

Default values: ?

The model implemented is:

(209)#\[\begin{equation} Nu = 0.2575 Re_b^{0.7}Pr{ -0.4564}Ja^{-0.2043} \end{equation}\]
(210)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu \times\frac{\lambda_l}{d_b} \frac{6max(\alpha_g,1e-4)}{d_b}, \end{equation}\]
(211)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = \begin{cases} Nu \frac{6\lambda_l}{d_b^2},\text{ if }\alpha_g> 1e-4,\\ 0,\text{ otherwise} \end{cases} \end{equation}\]
(212)#\[\begin{equation} \texttt{hi(k, n_l)} = 1e8, \end{equation}\]

with

  • \(Re_b=\frac{\rho_l d_b (u_g-u_l)}{\mu_l}\)

  • \(Pr\frac{\mu_l Cp_l}{\lambda_l}\)

  • \(Ja=\frac{\rho_lCp_l(T_g-T_l)}{\rho_gL_{vap}}\)

Ranz Marshall#

The model is also described in REFNEC and is implemented in:

void Flux_interfacial_Ranz_Marshall::set_param(Param& param)
{
param.ajouter("dv_min", &dv_min_);
}

Default values:

  • \(\texttt{a_min}= 0.01\).

The model implemented is:

(213)#\[\begin{equation} \mathit{Nu} = 2.0 + 0.6 \mathit{Re}_b^{0.5}\mathit{Pr}^{0.3} \end{equation}\]
(214)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu \times\frac{\lambda_l}{d_b} \frac{6\max(\alpha_g,\texttt{a_ min})}{d_b}, \end{equation}\]
(215)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = \begin{cases} \mathit{Nu} \frac{6\lambda_l}{d_b^2},\ \text{if}\ \alpha_g> \texttt{a_ min},\\ 0,\ \text{otherwise} \end{cases} \end{equation}\]
(216)#\[\begin{equation} \texttt{hi(k, n_l)} = 1e8, \end{equation}\]

with

  • \(Re_b=\frac{\rho_l d (u_g-u_l)}{\mu_l}\)

  • \(Pr = \frac{\mu_l Cp_l}{\lambda_l}\)

Wolfert#

The model is also described in REFNEC and is implemented in:

void Flux_interfacial_Wolfert::set_param(Param& param)
{
param.ajouter("Pr_t", &Pr_t_);
}

Default values:

  • \(\texttt{Pr_t_} = 0.85\).

The model implemented is:

(217)#\[\begin{equation} Nu = \frac{12}{\texttt{M_{PI}}} Ja +\frac{2}{\sqrt{\pi}}(1+\nu_t\rho_l \frac{Cp_l}{\lambda_l})Pe^{0.5}; \end{equation}\]
(218)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu \times \frac{\lambda_l}{d_b} \frac{6max(\alpha_g,1e-4)}{d_b}, \end{equation}\]
(219)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = \begin{cases} Nu \frac{6\lambda_l}{d_b^2},\text{ if }\alpha_g> 1e-4,\\ 0,\text{ otherwise} \end{cases} \end{equation}\]

with

  • \(Ja=\frac{\rho_l Cp_l (T_g-T_l)}{\rho_lLvap}\)

  • \(Pe\frac{\rho_l Cp_l (u_g-u_l)d}{\lambda_l}\)

  • \texttt{M_PI} = \(\pi\)

Wolfert compsant (To be erased)#

The model is also described in REFNEC and is implemented in:

void Flux_interfacial_Wolfert_composant::set_param(Param& param)
{
  param.ajouter("Pr_t", &Pr_t_);
  param.ajouter("dv_min", &dv_min_);
}

Default values:

  • \(\texttt{Pr_t_ = 0.85}\).

The model implemented is:

(220)#\[\begin{equation} Nu = \frac{12}{\texttt{M_{PI}}} Ja +\frac{2}{\sqrt{\texttt{M_{PI}}}}(1+\lambda_t\rho_l \frac{Cp_l}{\lambda_l})Pe^{0.5}; \end{equation}\]
(221)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu \times\frac{\lambda_l}{d} \frac{6max(\alpha_g,1e-4)}{d}, \end{equation}\]
(222)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = \begin{cases} Nu \frac{6\lambda_l}{d^2},\ if\ \alpha_g> 1e-4,\\ 0,\text{ otherwise} \end{cases} \end{equation}\]

with

  • \(Ja=\frac{\rho_l Cp_l (T_g-T_l)}{\rho_lLvap}\)

  • \(Pe=\frac{\rho_l Cp_l (u_g-u_l)d}{\lambda_l}\)

  • \(U_\tau = 0.1987 (u_g-u_l) (\frac{D_h\rho_l (u_g-u_l)}{\mu_l})^{-1/8}\)

  • \(\lambda_t = 0.06Pr_t U_\tau D_h \)

  • \texttt{M_PI} = \(\pi\)

Zeitoun#

The model is also described in REFNEC and is implemented in:

void Flux_interfacial_Zeitoun::set_param(Param& param)
{
param.ajouter("dv_min", &dv_min_);
  if (a_res_ < 1.e-12)
    {
      a_res_ = ref_cast(QDM_Multiphase, pb_->equation(0)).alpha_res();
      a_res_ = std::max(1.e-4, a_res_*10.);
    }
}

Default values:

  • \(\texttt{a_min_coeff} = 0.1\),

  • \(\texttt{a_min} = 0.01\),

  • \(\texttt{a_res_} = -1.\)

The model implemented is:

(223)#\[\begin{equation} Nu = 2.04Re_b^{0.61}max(\alpha_g, \texttt{a_min_coeff})^{0.328} Ja^{-0.308} \end{equation}\]

If \(( T_g > T_l)\) then:

(224)#\[\begin{equation} \texttt{hi(n_l, k)} = Nu *\frac{\lambda_l}{d_b} \frac{6max(\alpha_g,\texttt{a_min})}{d_b}, \end{equation}\]
(225)#\[\begin{equation} \texttt{da_ hi(n_l, k, k)} = da_{Nu} \frac{6\lambda_l}{d_b^2}max(\alpha_g,\texttt{a_min}) \begin{cases} Nu \frac{6\lambda_l}{d_b^2},\ if\ \alpha_g> \texttt{a_ min},\\ 0,\text{ otherwise} \end{cases} \end{equation}\]
(226)#\[\begin{equation} \texttt{ dp_hi(n_l, k)} = dP_{Nu} \frac{6\lambda_l}{d_b^2}\max(\alpha_g,\texttt{a_min}) \end{equation}\]
(227)#\[\begin{equation} \texttt{dT_hi(n_l, k,n_l)}= dT_{lNu} \frac{6\lambda_l}{d_b^2}\max(\alpha_g,\texttt{a_min}) \end{equation}\]
(228)#\[\begin{equation} \texttt{dT_hi(n_l, k, k)} = dT_{gNu} \frac{6\lambda_l}{d_b^2}\max(\alpha_g,\texttt{a_min}) \end{equation}\]
(229)#\[\begin{equation} \texttt{hi(k, n_l)} = 1e8; \end{equation}\]

And if \(\alpha_g < \text{a_res_}\) then:

(230)#\[\begin{equation} \texttt{hi(n_l, k)} = 1e8 \times(1-\frac{alpha_g}{\texttt{a_res_} }) + \texttt{hi(n_l, k)} \frac{alpha_g}{\texttt{a_res_} }; \end{equation}\]
(231)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = \frac{-1e8}{\texttt{a_res_} } + \texttt{da_hi(n_l, k, k)}\frac{\alpha_g}{\texttt{a_res_} } + \frac{\texttt{hi(n_l, k)}}{\texttt{a_res_} }; \end{equation}\]
(232)#\[\begin{equation} \texttt{dp_hi(n_l, k)} = \texttt{dp_hi(n_l, k)}\frac{\alpha_g}{\text{a_res_} } ; \end{equation}\]

End. Else (Temperature condition)

(233)#\[\begin{equation} \texttt{hi(n_l, k)} = 1e8, \end{equation}\]
(234)#\[\begin{equation} \texttt{da_hi(n_l, k, k)} = 0, \end{equation}\]
(235)#\[\begin{equation} \texttt{dp_hi(n_l, k)} = 0, \end{equation}\]
(236)#\[\begin{equation} \texttt{dT_hi(n_l, k,n_l)}= 0, \end{equation}\]
(237)#\[\begin{equation} \texttt{dT_hi(n_l, k, k)} = 0, \end{equation}\]
(238)#\[\begin{equation} \texttt{ hi(k, n_l)} = 1e8; \end{equation}\]

with

  • \(Re_b = \frac{\rho_l (u_g-u_l)d_b}{\mu_l}\)

  • \(Ja=\frac{max(T_g-T_l,2.)\rho_l Cp_l}{\rho_lLvap}\)

  • \(dP_{Ja}=\frac{max(T_g-T_l,2.)\rho_l Cp_l}{\rho_l}\frac{-dP_{vap}}{Lvap^2}\)

  • \(dT_{gJa}=\begin{cases}\frac{\rho_lCp_l}{\rho_gLvap},\ if\ T_g-T_l> 2.\\ 0,\text{ otherwise} \end{cases}\)

  • \(dT_{lJa}=\begin{cases}\frac{-\rho_lCp_l}{\rho_gLvap},\ if\ T_g-T_l> 2.\\ 0,\text{ otherwise}\end{cases}\)

  • \(da_{Nu} = 2.04 Re_b^{0.61}Ja^{-1.308}\begin{cases} 0.328(\alpha_g^{0.328-1},\text{ if }\alpha_g > \texttt{a_min_coeff}\\ 0,\text{ otherwise} \end{cases}\)

  • \(dP_{Nu} = 2.04Re_b^{0.61} \max(\alpha_g, \texttt{a_min_coeff})^{0.328} -0.308dP_{Ja} Ja^{-1.308}\)

  • \(dT_{gNu} = 2.04Re_b^{0.61} \max(\alpha_g, \texttt{a_min_coeff})^{0.328} -0.308dT_{Ja} Ja^{-1.308}\)

  • \(dT_{lNu} = 2.04Re_b^{0.61} \max(\alpha_g, \texttt{a_min_coeff})^{0.328} -0.308dT_{Ja} Ja^{-1.308}\)

Wall heat flux#

The general expression of the wall heat flux is:

(239)#\[\begin{equation} q_{pk} \end{equation}\]

The model is implemented in:

void Flux_parietal_base::set_param(Param& param)

The available input parameters are:

    int N;                // Number of phases
    int f;                // face number
    double y;             // distance between the face and the center of gravity of the cell
    double D_h;           // Hydraulic diameter
    double D_ch;          // Heated hydraulic  diameter
    double p;             // Pressure
    double Tp;            // Wall temperature
    const double *alpha;  // Void fraction
    const double *T;      // Temperature
    const double *v;      // Velocity norm
    const double *lambda; // Thermal conductivity
    const double *mu;     // Viscosity
    const double *rho;    // Density
    const double *Cp;     // Calorific capacity
    const double *Lvap;   // Latent heat
    const double *Sigma;  // Surface tension
    const double *Tsat;   //Phase change saturated temperature

The interfacial heat flux operator must fill qpk and qpi tabs and there derivative so that:

  • \(\texttt{qpk}\) heat flux

  • \(\texttt{da_qpk}\) heat flux derivative regarding void fraction

  • \(\texttt{dp_qpk}\) heat flux derivative regarding pressure

  • \(\texttt{dv_qpk}\) heat flux derivative regarding velocity

  • \(\texttt{dTf_qpk}\) heat flux derivative regarding temperature

  • \(\texttt{dTp_qpk}\) heat flux derivative regarding wall temperature

  • \(\texttt{qpi}\) phase change heat flux

  • \(\texttt{da_qpi}\) phase change heat flux derivative regarding void fraction

  • \(\texttt{dp_qpi}\) phase change heat flux derivative regarding pressure

  • \(\texttt{dv_qpi}\) phase change heat flux derivative regarding velocity

  • \(\texttt{dTf_qpi}\) phase change heat flux derivative regarding temperature

  • \(\texttt{dTp_qpi}\) phase change heat flux derivative regarding wall temperature

  • \(\texttt{d_nuc}\) nucleation diameter

Availability of interfacial heat flux partitioning models in TrioCFD/CMFD:

Model

Used

Validated

Test case

Kommajosyula

Yes

No

Kurul-Podowski

Yes

Yes

TrioCFD/CoolProp

Kommajosyula (to be erased)#

The model is described in Kommajosyula [Kom20] and is implemented in:

void Flux_parietal_Kommajosyula::set_param(Param& param)
{
  param.ajouter("contact_angle_deg",&theta_,Param::REQUIRED);
  param.ajouter("molar_mass",&molar_mass_,Param::REQUIRED);
}

{\color{red} Warning}: the model was implemented but dropped because we could not fit the original data and so is not validated.

Kurul Podowski#

The model is described in Kurul [Kur91] and depicted in Figure 5.

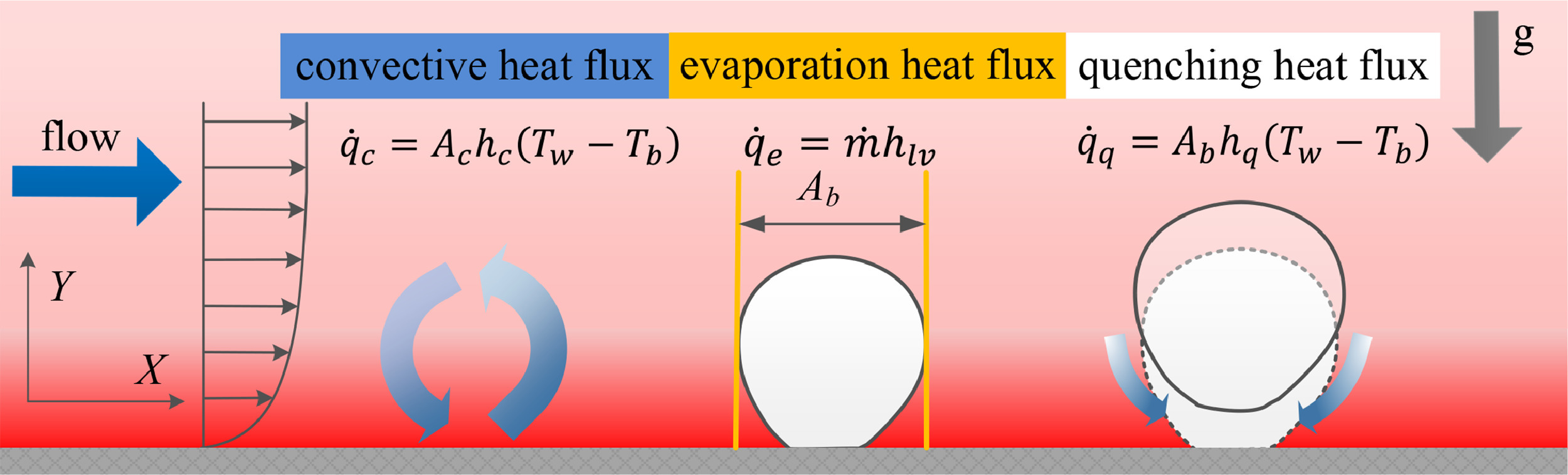
wall heat fluw from Kurul

Figure 5 Depiction of the wall heat flux partitioning model for subcooled flow boiling from Zhou et al. [ZHG+21].#

The model is implemented in:

void Flux_parietal_Kurul_Podowski::set_param(Param& param)

The model implemented is decomposed as follows:

First, we have a Correction of single phase heat flux

  • \(\texttt{qpk}=\texttt{qpk}_{single\ phase}(1-A_{bub})\),

  • \(\texttt{da_qpk}=\texttt{da_qpk}_{single\ phase}(1-A_{bub})\),

  • \(\texttt{dp_qpk}=\texttt{dp_qpk}_{single\ phase}(1-A_{bub})\),

  • \(\texttt{dv_qpk}\texttt{=dv_qpk}_{single\ phase}(1-A_{bub})\),

  • \(\texttt{dTf_qpk}=\texttt{dT_f_qpk}_{single\ phase}(1-A_{bub})\),

  • \(\texttt{dTp_qpk}=\texttt{dTp_qpk}_{single\ phase}(1-A_{bub})\).

Then, we add the partitioned heat flux

  • \(\texttt{dTp_qpk} \pluseq -\texttt{qpk}_{single\ phase}(1-A_{bub})\frac{dA_{bub}}{dT_p}+\frac{dq_{quench}}{dT_p}\),

  • \(\texttt{qpk} \pluseq q_{quench}\),

  • \(\texttt{dTf_qpk} \pluseq \frac{dq_{quench}}{dT_l}\),

  • \(\texttt{qpi} \pluseq q_{evap}\),

  • \(\texttt{dTp_qpi} \pluseq \frac{dq_{evap}}{dT_p}\), with

  • Evaporation flux \(q_{evap}=f_{dep}\frac{\pi d_b^3}{6}\rho_gL_{vap}N_{sites}\)

  • Evaporation flux derivative regarding wall departure \(\frac{dq_{evap}}{dT_p} =(\frac{df_{dep}}{dT_p}\frac{\pi d_b^3}{6}N_{sites}+f_{dep}\frac{3\pi d^2}{6}\frac{dd_b}{dT_p}N_{sites}+f_{dep}\frac{\pi d_b^3}{6}\frac{dN_{sites}}{dT_p})\rho_g L_{vap}\).

  • Quenching flux \(q_{quench}=A_{bub}\sqrt{f_{dep}}\frac{2\lambda_l(T_p-T_l)}{\sqrt{\frac{\pi \lambda_l}{\rho_l Cp_l}}}\).

  • Quenching flux derivative regarding liquid temperature \(\frac{d q_{quench}}{d T_l} =A_{bub}\sqrt{f_{dep}}\frac{-2\lambda_l}{\sqrt{\frac{\pi \lambda_l}{\rho_l Cp_l}}}\).

  • Quenching flux derivative regarding wall temperature \(\frac{d q_{quench}}{d T_p} =\frac{d A_{bub}}{dT_p} \sqrt{f_{dep}}\frac{-2\lambda_l}{\sqrt{\frac{\pi \lambda_l}{\rho_l Cp_l}}}+A_{bub}\sqrt{f_{dep}}\frac{2\lambda_l}{\sqrt{\frac{\pi \lambda_l}{\rho_l Cp_l}}}-A_{bub}\frac{1}{2}\frac{df_{dep}}{dT_p}\frac{1}{\sqrt{f_{dep}}}\frac{2\lambda_l(T_p-T_l)}{\sqrt{\frac{\pi \lambda_l}{\rho_l Cp_l}}}\).

  • Number of evaporation sites \(N_{sites}=(210\times{}(T_p-T_{sat}))^{1.8}\).

  • Number of evaporation sites \(N_{sites}=(210\times{}(T_p-T_{sat}))^{1.8}\).

  • Number of evaporation sites derivative regarding wall temperature \(\frac{d N_{sites}}{dT_p} =210\times 1.8(210.(T_p-T_{sat}))^{0.8}\).

  • Wall bubble diameter \(d_b=0.0001(T_p-T_{sat})+0.0014\).

  • Wall bubble diameter derivative regrading wall temperature \(\frac{dd_b}{dT_p}=0.0001\).

  • Wall bubble total area \(A_{bub}=min(1.,\frac{\pi N_{sites}d_b^2}{4})\).

  • Wall bubble total area derivative regarding wall temperature \(\frac{dA_{bub}}{dT_p} =\frac{\pi d_b^2}{4}\frac{d N_{sites}}{dT_p} + \frac{\pi d_b N_{sites}}{2}\frac{d d_b}{dT_p}\), if \(A_{bubbles}\neq 1.\), \(0\), otherwise.

  • Departure frequency \(f_dep=\sqrt{\frac{4}{3}\frac{9.81(\rho_l-\rho_g)}{\rho_l}}d_b^{-0.5}\).

  • Departure frequency derivative regarding wall temperature \(\frac{d f_dep}{d T_p}=-0.5\frac{dd_b}{dT_p}d^{-1.5}\sqrt{\frac{4}{3}\frac{9.81(\rho_l-rho_g)}{\rho_l}}\)

Phase change#

The general expression of the phase change mass flux is:

(240)#\[\begin{equation} G(\alpha,p,T) \end{equation}\]

It needs to be considered when there is a kinetic limit of gas for the phase change, for liquid metals, for example, but it does not apply to water.

The model is implemented in:

void Changement_phase_base::set_param(Param& param)

The available input parameters are:

    double D_h;           // Hydraulic diameter
    double p;             // Pressure
    const double *alpha;  // Void fraction
    const double *T;      // Temperature
    const double *lambda; // Thermal conductivity
    const double *mu;     // Viscosity
    const double *rho;    // Density
    const double *Cp;     // Calorific capacity
    const double *Lvap;   // Latent heat
    const double *Tsat;   //Phase change saturated temperature

The phase change mass flux operator must fill dT_G, da_G, dp_G tabs and there derivative so that:

  • \(\texttt{G}\) mass flux

  • \(\texttt{dT_G}\) mass flux derivative regarding temperature

  • \(\texttt{dp_G }\) mass flux derivative regarding pressure

  • \(\texttt{da_G}\) mass flux derivative regarding void fraction

Silver Simpson#

The model is also described in Silver and Simpson (1949, not found) and is implemented as:

void Changement_phase_Silver_Simpson::set_param(Param& param)
{
  param.ajouter("lambda_e", &lambda_ec[0]); multiplicative factor for evaporation
  param.ajouter("lambda_c", &lambda_ec[1]); //  multiplicative factor for condensation
  param.ajouter("alpha_min", &alpha_min); // minimal void fraction to activate phase change
  param.ajouter("M", &M, Param::REQUIRED); // molar mass of steam
}

Default values:

  • \(\texttt{lambda_ec[2]} = { 1, 1 }\),

  • \(\texttt{M} = -100.\),

  • \(\texttt{alpha_min} = 0.1\).

The model implemented is:

(241)#\[\begin{align} &\texttt{dT_G}_g = \texttt{fac} \times \texttt{var_a} \times \frac{dT_{Psat}(T_g) - 0.5 \times \frac{Psat(T_g)}{T_g + T_0}}{\sqrt{T_g + T_0}}\\ &\texttt{dT_G}_l = \texttt{fac} \times \texttt{var_a} \times 0.5 \times P \times (T_l + T_0)^{-1.5}\\ &\texttt{da_G}_g = \begin{cases} \texttt{fac} \times \texttt{var_T} \times \texttt{var_al}, if\ \alpha_g > \text{alpha_min}, \\ 0,\text{ otherwise}.\end{cases}\\ &\texttt{da_G}_l = \begin{cases} \texttt{fac} \times \texttt{var_T} \times \texttt{var_ak} \times 1.5 \times \sqrt{\alpha_l}, if\ \alpha_l > \texttt{alpha_min},\\ 0,\ \text{otherwise}. \end{cases}\\ &\texttt{dp_G} = - \texttt{fac} \times \frac{\texttt{var_a}}{\sqrt{T_l + T_0}}\\ &\texttt{G} = \texttt{fac} \times\texttt{ var_ak} \times \texttt{var_al} \times \texttt{var_T}; \end{align}\]

with

  • \(T_0 = 273.15\),

  • \(\texttt{var_ak}=\max(\alpha_g, \texttt{alpha_min})\),

  • \(\texttt{var_al}=\parent{\max\parent{\alpha_l,\texttt{alpha_min}}}^{1.5}\),

  • \(\texttt{var_a}=\texttt{var_ak} \times \texttt{var_al}\),

  • \(\texttt{var_T} = \frac{Psat(T_g)}{\sqrt{T_g + T_0}} - \frac{P}{\sqrt{T_l + T_0}}\),

  • \(\texttt{fac} = \lambda_{ec}[var_T < 0] \frac{4}{D_h}\sqrt{\frac{\texttt{M}}{2\texttt{M_{PI}}8.314}}\)

Contents